Consensus Clustering
This post is mainly based on
- Cluster ensembles – a knowledge reuse framework for combining multiple partitions
- Consensus Clustering: A Resampling-Based Method for Class Discovery and Visualization of Gene Expression Microarray Data
Proposed in 2002, consensus clustering aims to combine results/labels from multiple clustering algorithms into a single consolidated clustering, without accessing the algorithms themselves. The proposed learning framework is called cluster ensembles. The optimization goal is to ensure the combined clustering is “similar” to each individual clustering. One of the key challenge faced by consensus clustering is reducing the computation cost.
A variant of the consensus clustering is Monti Consensus Clustering, which is commonly used to determine the number of clusters $k$. It can also be used to evaluate the stability of clusters. The idea is similar bagging: run the same clustering algorithm on multiple datasets resampled from the original one.
Consensus Clustering
Let $X = \{ x_1, x_2, …, x_n \}$ be the dataset with $n$ points. A clustering algorithm divide $X$ into $k$ partitions $\{ C_1, …, C_k \}$. Alternatively, we can express the partition as a label vector $\lambda \in [1, …, k]^n$, where dimension $i$ representation point $x_i$ and its value represent the class of $x_i$. A clusterer $\Phi$ is a function that generate a partition $\lambda$ from the data.
The consensus clustering algorithm maps a set of $r$ labelings $( \lambda_1, …, \lambda_r )$ into a single labeling $\lambda$, using a consensus function $\Gamma$.
Recall that the goal of consensus clustering is to create a $\lambda$ that is “similar” to each $\lambda_i$. To achieve this goal, we need to solve 2 problems: permutation invariance of the labeling and similarity measure.
Permutation Invariance
Consider two clusters $\lambda_1 = (1, 1, 1, 2, 2, 3, 3)$ and $\lambda_2 = (2, 2, 2, 3, 3, 1, 1)$. Although the label vector $\lambda_1$ and $\lambda_2$ are different, the partition they generated are logically equivalent. The permutation law suggest that for a clustering with $k$ classes, there are $k!$ different label vectors for the same partition. This permutation problem could be solved by Hypergraph: instead of looking at cluster index, we check which group of points shared the same hyperedge.
Similarity Measure
The authors proposed to use mutual information (MI) to measure the similarity between $\lambda$ and $\lambda_1, …, \lambda_r$. In other words, we assume there exists a ground truth distribution that generate all $\lambda_i$.
Let $\Lambda = (\lambda_1, …, \lambda_r)$. Define the average normalized mutual information (ANMI) as:
\[\phi^{(ANMI)}(\Lambda, \hat{\lambda}) = \frac{1}{r} \sum_{q=1}^r \phi^{NMI}(\hat{\lambda}, \lambda_q)\]For details on normalized mutual information $\phi^{NMI}$, please refer to the paper.
The optimization goal is:
\[\lambda^* = \operatorname{argmax}_{\hat{\lambda}} \phi^{(ANMI)}(\Lambda, \hat{\lambda})\]i.e., consensus function seek a clustering that shares the most information with the original $r$ clusterings.
Greedy Optimization
The above optimization problem is not easy to solve: a brute force approach needs to search around $\frac{k^n}{k!}$ possible combinations for $n \gg k$. For clustering 16 points into 4 classes, the number of combinations is $171,798,901$.
To solve this computational cost problem, the authors proposed 3 approaches:
- Cluster-based Similarity Partitioning Algorithm (CSPA)
- HyperGraph Partitioning Algorithm (HGPA)
- Meta-CLustering Algorithm (MCLA)
For CSPA, a $n \times n$ similarity matrix $S$ can be computed from the hypergraph $S = \frac{1}{r} H H^\top$, where each entry represent the fraction of clusterings in which two objects are in the same cluster. Partition can be computed from this similarity matrix. For details on how to derive $S$ from hypergraph or how to compute partitions from $S$, please refer to the paper. Complexity for CSPA is $O(n^2kr)$, HGPA is $O(nkr)$, and MCLA is $O(nk^2r^2)$. In practice $n \gg k,r$, hence CSPA is least computational efficient algorithm.
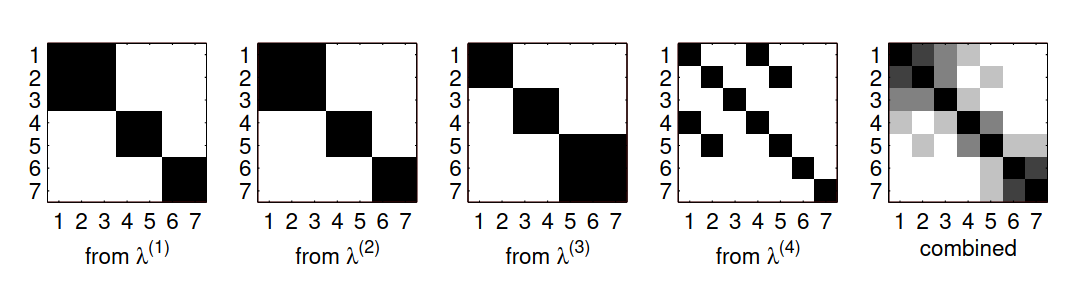 Cluster-based similarity partitioning algorithm (CSPA) for the cluster ensemble. Each clustering contributes a similarity matrix. Matrix entries are shown by darkness proportional to similarity. Their average is then used to recluster the objects to yield consensus.
Cluster-based similarity partitioning algorithm (CSPA) for the cluster ensemble. Each clustering contributes a similarity matrix. Matrix entries are shown by darkness proportional to similarity. Their average is then used to recluster the objects to yield consensus.
Monti Consensus Clustering
Monti consensus clustering was proposed in 2003 for class discovery and clustering validation on gene expression data. The goal is to use resampling techniques to assess the stability of the discovered clusters / sensitivity to the initial condition. The authors proposed summary statistics and visualization techniques to: (1) help determine the number of clusters (2) quantify the confidence on derived clusters. The inspection of the visualized data can often help gain additional insight into the recommendations returned by the algorithm.
The intuition is: if the dataset $X$ is generated from distinct distributions, resampling $X$ should produce samples that still induce those distinct distributions. Therefore, the derived cluster should be relatively stable. However, if $X$ is NOT generated from distinct distributions, resampling $X$ should cause the clustering algorithm to output radically different results. Hence the consensus between different samples are low.
Consensus matrix reordering and visualization
Consensus matrix is computed by an algorithm similar to CSPA. The resulting consensus matrix used to construct a hierarchical tree to yield a dendogram of point adjacencies. This hierarchical tree is used to reorder the similar points to form block-diagonal matrix. For details in leaf-ordering algorithm, please check the original paper.
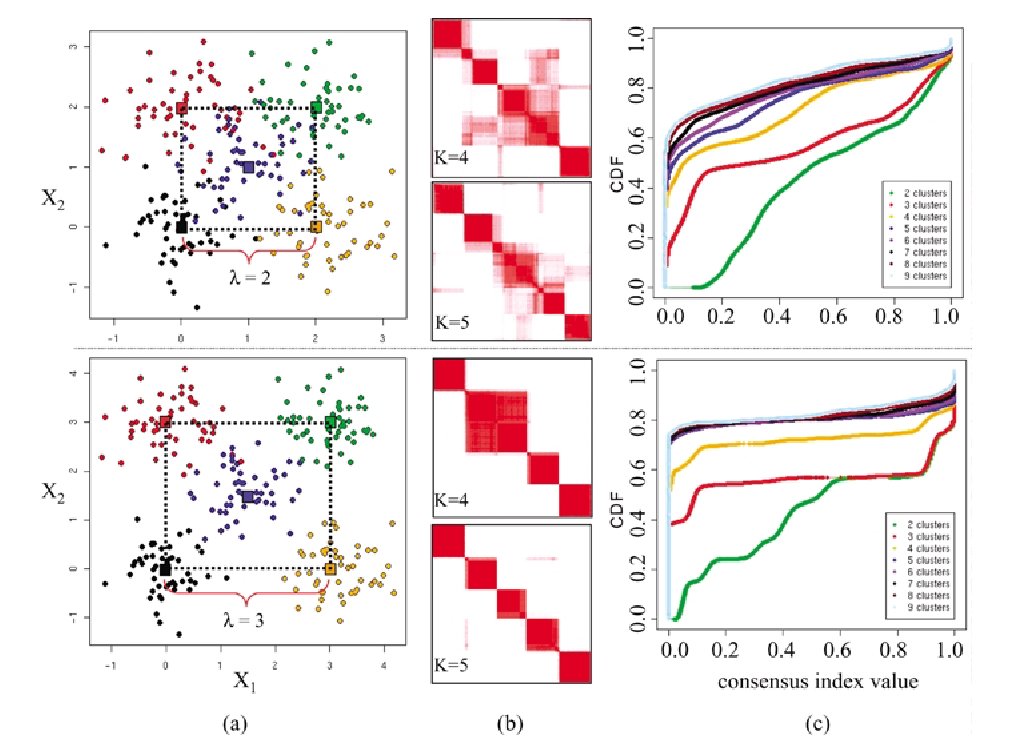
Results of consensus clustering applied to the simulated data Gaussian5 with distance $\lambda$ between Gaussians’ centers $\lambda = 2$ (top) and $\lambda = 3$ (bottom): (a) raw data; (b) consensus matrices M(K ) for K = 4, 5; and (c) CDF plots corresponding to the consensus matrices in the range K = 2, 3, … , 9.
Consensus summary statistics
Let $M$ be the consensus matrix. For each cluster $k$ and each point $i \in I_k$ in cluster $k$, define
\[\text{cluster consensus: } m(k) = \frac{1}{N_k(N_k-1)/2}\sum_{i,j, i<j} M(i,j)\] \[\text{item consensus: } m_i(k) = \frac{1}{N_k - \mathbb{1}\{ i \in I_k \}}\sum_{j \in I_k, j\not=i} M(i,j)\]The cluster consensus $m(k)$ measures the average consensus for all unique pair of points in the cluster. The item consensus $m_i(k)$ measures the average consensus between point $i$ and all the other points in cluster $k$.
Define,
\[\text{consensus distribution: } P(i,j) \text{ , s.t., } M(i,j) \sim P(i,j)\] \[\text{empirical cumulative distribution: } \text{CDF}(c) = \frac{\sum_{i<j} \mathbb{1}\{ M(i,j) \leq c \} }{ N(N-1)/2 }\]Let $A(K)$ be area under curve (AUC) for number of cluster $K$,
\[\text{Delta AUC: } \Delta(K) = \begin{cases} A(K) & \text{if } K=2 \\ \frac{A(K+1) - A(K)}{A(K)} & \text{if } K>2 \end{cases}\]The intuition is: assume to entries of the consensus matrix $M$ is sampled from a distribution $P$. When the clustering is stable, $P(i,j)$ should be close to 0 or 1 (a pair of points $i,j$ either belongs to the same cluster with high confidence or not belongs to the same cluster with high confidence). Consider figure (b) above, for a well-defined clustering, the CDF curve should jump at consensus index value close to 0 or 1, and remain relatively flat between 0 and 1. $\Delta(K)$ defines quantifies the concentration of the consensus distribution.
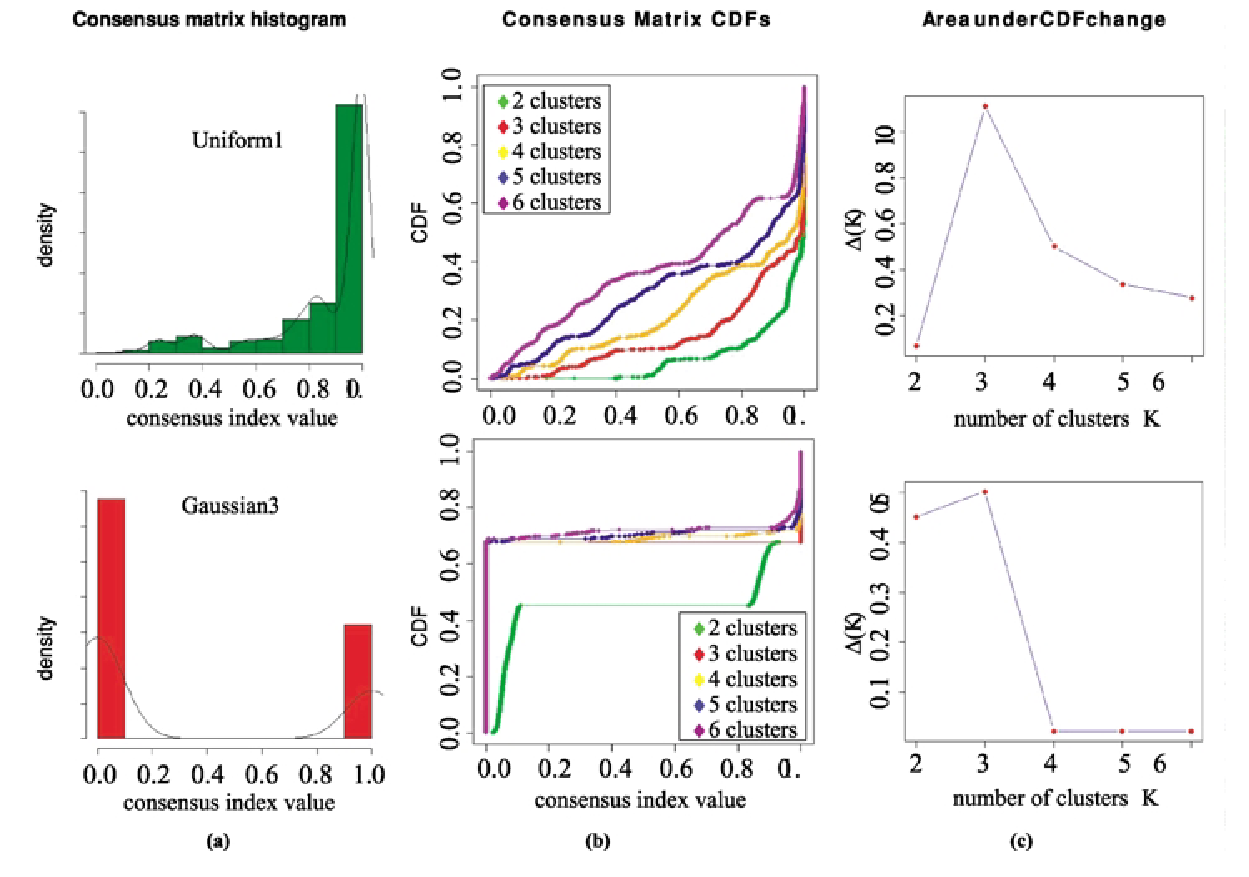
Measuring consensus for different $K$ on the simulated datasets of Uniform1 and Gaussian3: (a) histograms of the entries of the consensus matrices with 3 clusters $M^{(3)}$; (b) empirical CDFs corresponding to the entries of consensus matrices with $K$ clusters $M^{(K)}$ for $K = 2, 3, … , 6$; (c) proportion increase $\Delta(K)$ in the area under the CDF.
Determining the number of clusters
Procedure
- Construct a consensus matrix $M^K$ for each of a series of cluster numbers $(K = 2, 3, . . . , K_{max})$
- Inspect the block matrices and select the $k$ corresponding to the the most well defined block matrix
- Inspect consensus summary statistics
- Select $K$ whose CDF shape is close to bimodal
- Select the largest $K$ that induces a large enough $\Delta(K)$