Pointer Networks
This post is mainly based on
Pointer Networks aim to solve a collection of combinatorial optimization problems which can be view as seq2seq modelling. These problems include:
- Planar convex hulls
- Delaunay triangulations
- Planar Travelling Salesman Problem (TSP)
The difference between a Pointer Network and a RNN-based Neural Machine Translation (NMT) model is: RNN based architecture requires a fixed vocabulary (e.g., rank 1-4 in the convex hull example below), whereas the “vocabulary” for a Pointer Network is the input sequence. In other words, each element of the output sequence points to an element of the input sequence, allowing the Pointer Network to produce a variable “vocabulary” sequence.
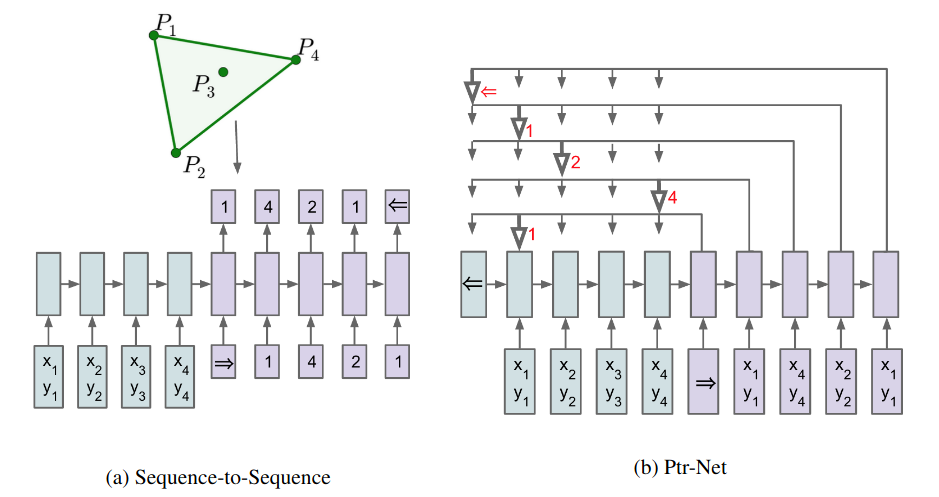
Convex hulls problem. Left: RNN-based encoder-decoder architecture, where the output dimensionality is fixed. Right: Pointer Network that produce output sequence using attention mechanism. $\Leftarrow$ represent the end token.
Problem Setup
Let:
- Input: $\mathcal{P} = (P_1, …, P_n) $ be a sequence of $n$ points/vectors.
- Output: $C = (C_1, …, C_m)$ be a sequence of indices, with length $m$
- $C_i \in { 1, …, n }$ indicating a pointer
Then we can estimate the conditional probability of the output sequence $C$ by:
\[P(C |\mathcal{P}; \theta) = \prod_{i=1}^m p_\theta( C_i | C_1, ..., C_{i-1}, \mathcal{P}; \theta )\]where $p_\theta$ is a the conditional probability estimated by a parametric model $p_\theta$ (e.g., an RNN).
The optimization goal is:
\[\theta^* = \underset{\theta}{\operatorname{argmax}} \sum_{\mathcal{P}, C} \log P(C | \mathcal{P}; \theta)\]i.e., the maximize the expected log probability under the training set.
Attention Mechanism
Pointer network is directly connected with the RNN with Attention architecture: it removes the context vector and directly use the soft-attention vector to compute loss.
RNN with Attention
I slightly changed the notation. Let:
- $(e_1, … , e_n)$ be the encoder hidden state
- $(d_1, … , d_m)$ be the decoder hidden state
- $v, W_1, and W_2$ be the learnable parameters of the attention module
Then the un-normalized attention vector $u_i$ of decoder state $i$ to encoder state $j$ is:
\[u_i^j = v^\top \tanh (W_1 e_j + W_2 d_i)\]The attention is $a_i$:
\[a_i^j = \operatorname{softmax}(u_i^j)\]The context vector $d_i’$:
\[d_i' = \sum_{j=1}^n a_i^j e_j\]Note that the above attention operation has $O(mn)$ complexity for an output sequence of length $m$.
The context vector $d_i’$ is concatenate to the previous decoder hidden state $d_i$ to compute output.
Pointer Network
For Pointer Network, we remove all steps after the attention vector:
\[p(C_i|C_1, ... , C_{i−1}, \mathcal{P}) = a_i\]We can use the above distribution $a_i$ and ground truth $C_i^*$ to compute the cross entropy loss.
Experiments
All experiments as conduct in 2-D space.
For the convex hull problem, the Point Network can produce good approximate solutions. It also generalize well (train on 50 points and test on 500 points; approximate solution covers 99.2% area of the optimal solution).
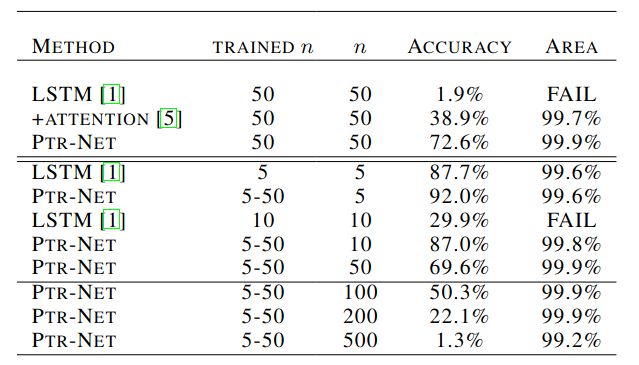
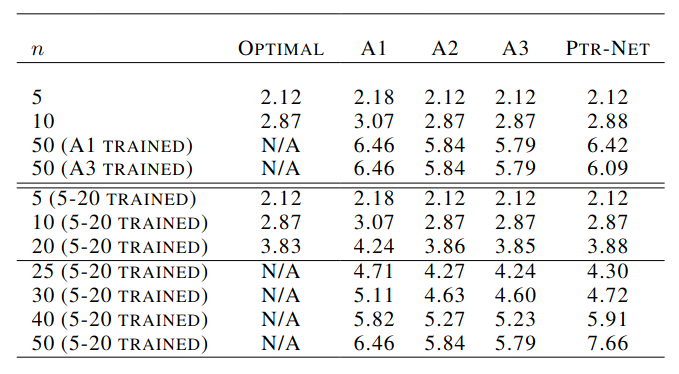
For the TSP problem, exact solution has $O(2^n n^2)$ complexity. Due to the complexity, optimal solution above n=20 is not provided and the model is trained on approximate solutions.
A1-A3 are approximate algorithms, with A1 and A2 has $O(n^2)$ complexity. A3 has $O(n^3)$ complexity, but its solution is bounded by 1.5x of the optimal length. The Point Network approximate optimal solution up to n=10. It cannot generalize above n=30 when training with n=20.
Additional problems: for n>20, where at least 10% of instances would not produce any valid tour.
Complexity
For the convex hull problem, the exact solutions requires $O(n \log n)$, where the pointer networks have complexity $O(mn)$
For TSP problem, the pointer networks have complexity $O(n^2)$, which does not makes it very attractive given A2’s performance and $O(n^2)$ complexity.
Discussion
Since all experiments are conducted in 2-D space, I’m curious about its relative performance in higher dimension / if there is approximation algorithm for convex hull in higher dimension space.
Another use case is using the Pointer Network as a differentiable module in a end-to-end control system, where it can select actions/options. This requires the action selection, or the $\operatorname{argmax}$ to be differentiable (e.g., Gumbel-Softmax). Example of this include AlphaStar, which uses the pointer network to manage the agent’s combinatorial large action space.