Normalization Layer
This post is mainly based on
- Layer Normalization, 2016
- Weight Normalization: A Simple Reparameterization to Accelerate Training of Deep Neural Networks, NIPS 2016
- Group Normalization, ECCV 2018
Also check: Batch Normalization post.
There are many types of normalization layer. The core idea is to performs the Z-Standardization operation:
\[z = \frac{x- \mu}{\sigma}\]Since we do not have access to the population, the main difference between them is how $\mu$ and $\sigma$ are estimated:
- Batch Norm: by a batch of $N$ points in a single channel
- Layer Norm: by one point across all channels
- Instance Norm: by one point in a single channel
- Group Norm: by one point across a group of channels
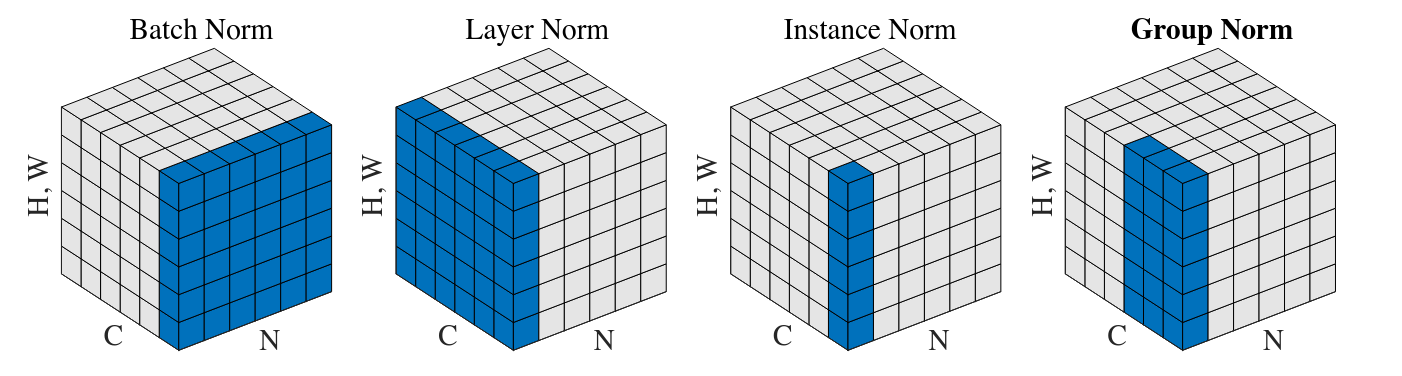
Normalization methods. Each subplot shows a feature map tensor, with N as the batch axis, C as the channel axis, and (H, W) as the spatial axes. The pixels in blue are normalized by the same mean and variance.
Let $X = (x_1, … x_N)$ be the input batch, where $x_i^j \in \mathbb{R}$ is the $j$-th channel / neuron of the $i$-th point. There all $C$ channels in total. Since $x_i^j$ is a scaler, there is no $W,H$ dimension (to simplify the discussion).
Batch Normalization
\[\mu_j = \frac{1}{N} \sum_{i=1}^N x_i^j\] \[\sigma_j^2 = \frac{1}{N} \sum_{i=1}^N (x_i^j - \mu_j)^2\] \[y^j = \frac{x^j - \mu_j}{\sigma_j}\]The normalization is performed on a per channel basis.
Note that a formal Batch Normalization also contains two learnable $\gamma$ and $\beta$ which scales and shift the output $y$. We ignore them for simplicity.
Problem of Batch Normalization:
- Ineffective in small batch training or distributed training (sample size too many)
- Not compatible with RNN or variable length data
- Suppose 1 sequence is significantly longer than the rest
- Other sequences will be zero-padded
- Compute $\mu, \sigma$ for padded sequences does not make sense
- Layer Normalization paper suggested that applying batch normalization to RNNs appears to require different statistics for different time-steps
Layer Normalization
\[\mu_i = \frac{1}{C} \sum_{j=1}^N x_i^j\] \[\sigma_i^2 = \frac{1}{C} \sum_{j=1}^N (x_i^j - \mu_i)^2\] \[y_i = \frac{x_i - \mu_i}{\sigma_i}\]The normalization is performed on a per sample basis.
Instance Normalization
Since $x_i^j \in \mathbb{R}$, $W,H$ collapse to a single value. Hence Instance Normalization output
\[y = x\]If $W,H$ does not collapse to a single value, for example, the output of convolution layer is a tensor with dimension $W \times H \times C$, then Instance Normalization compute $\mu, \sigma$ for a single point, in a single channel, across a $H \times W$ matrix.
Group Normalization
The idea of Group Normalization is:
- Layer Normalization and Instance Normalization are too extreme
- The first normalize across all channels
- The second does not normalize across channels at all
- Group Normalization
- Generalizes Layer / Instance Normalization
- Normalize across a set of features $(G_1, …, G_M)$
- Each $G_k$ is a set of channels
- Requires a hyperparameter $M$, $G = 32$ by default
- Group size: $|G_k| = C/M$
For the $k$-th group $G_k$, compute group mean and variance for a single point, across channels:
\[\mu_{i,k} = \frac{1}{|G_k|} \sum_{j \in G_k} x_i^j\] \[\sigma_{i,k}^2 = \frac{1}{|G_k|} \sum_{j \in G_k} (x_i^j - \mu_{i,k})^2\]For each point $i$ and channel $j \in G_k$
\[y_i^j = \frac{x_i^j - \mu_{i,k}}{\sigma_{i,k}}\]Groups are pre-defined. The idea is that as learning progress, channels in the same group will self-organize to learn features with same mean and variance. Different groups allow features of different mean and variance to be learned (e.g., for CV problems, Conv filter could extract frequency, shapes, illumination, texture features, which have drastically different $\mu, \sigma$).
Weight Normalization
Technically speaking, Weight Normalization is not a layer. All the above normalization techniques modifies the data. Weight Normalization modifies the model parameter. This is evident from pytorch’s implementation:
- All the above normalization techniques are implemented under torch.nn (link)
- Weight Normalization is implemented under torch.nn.utils (link)
- Implemented via a hook that recomputes the weight tensor from the magnitude and direction before every forward() call.
The idea is to reparameterizing the weights $w$ into direction $\frac{v}{\|v\|}$ and scale $g$:
\[w = g \frac{v}{\|v\|}\]The automatic differentiation, compute gradient of loss w.r.t. $g$ and $v$, rather than $w$. The authors mentioned that the reparameterization improves the conditioning of the optimization problem and presented their analysis in Section 2.1.
Some articles online claim that Weight Normalization is significantly less stable compared to Batch Normalization in training of deep networks, hence is not widely used. It is worth noting that the TCN paper in 2018 also adopted Weight Normalization. Personally, I found the performance to be mixed. For WN vs BN, the result depends on many factors, including:
- If the input is discrete
- If the sequence have uniform length
- If the each time step $t$ is inherently different ($t$ in a sentence vs $t$ in a sample of time series)