Transformer

This post is mainly based on

• Attention Is All You Need, NIPS 2017
• Dr. Krzysztof Choromanski’s Lectures
• Harvard NLP’s The Annotated Transformer
• Jake Tae’s blog

Transformer is an architecture that is built on Attention.

Attention

Recall an Attention layer maps an input sequence $x_1, …, x_n$ to a contextualized embedding $z_1, …, z_n$

We need to distinguish between Self-Attention, Cross-Attention, and Causal-Attention:

• Self-Attention
  • Only consider the target sequence (length $L$)
  • e.g., language model
• Cross-Attention
  • Consider both the target sequence (length $L$) and the source sequence (length $M$)
  • e.g., story completion
  • The source sequence is the prompt and the target sequence is the generated text
  • Self-Attention can be viewed as a special case of Cross-Attention where the source sequence is the target sequence itself
• Causal-Attention
  • The model can only observe elements in the sequence before current element
  • e.g., time series prediction
  • Implemented by masking unobserved elements

A forward pass on attention layer consists of a series of matrix multiplications.

Cross-Attention

Consider the input data:

• Source sequence: $y_1, …, y_M \in \mathbb{R}^d$, $d$-dimensional vectors
• Target sequence: $x_1, …, x_L \in \mathbb{R}^d$, $d$-dimensional vectors
• Write them in a matrices $Y \in \mathbb{R}^{M \times d}, X \in \mathbb{R}^{L \times d}$

The model parameters:

• Query projection matrix: $W_q \in \mathbb{R}^{d \times d’}$
• Key projection matrix: $W_k \in \mathbb{R}^{d \times d’}$
• Value projection matrix: $W_v \in \mathbb{R}^{d \times d}$
• $d’$ is the dimension of intermediate representation

Project the input $X,Y$ onto some latent space:

• Query: $ Q = X W_q \in \mathbb{R}^{L \times d’} $
• Key: $ K = Y W_k \in \mathbb{R}^{M \times d’} $
• Value: $ V = Y W_v \in \mathbb{R}^{M \times d} $

Compute cross-attention matrix $A_{norm}$:

\[A_{norm} = \operatorname{softmax}\left( \frac{Q K^\top}{ \sqrt{ d' } } \right)\]

Alternatively, we can write $A_{norm}$ as:

\[A = \exp \left( \frac{Q K^\top}{ \sqrt{ d' } } \right) \in \mathbb{R}^{L \times M}\] \[\left[ A_{norm} \right]_{ij} = \frac{A_{ij}}{ \sum_{m=1}^M A_{im} }\]

where $\exp$ is element wise exponentiation. The reason why we want to write $A_{norm}$ as $A$ will be discussed in the kernel function section below.

Compute output matrix $X’$:

\[X' = A_{norm} V \in \mathbb{R}^{L \times d}\]

Self-Attention

Setting the source sequence as the target sequence ($Y=X$) yields Self-Attention:

• $X \in \mathbb{R}^{L \times d}$

…

Compute the intermediate representations:

• Query: $ Q = X W_q \in \mathbb{R}^{L \times d’} $
• Key: $ K = X W_k \in \mathbb{R}^{L \times d’} $
• Value: $ V = X W_v \in \mathbb{R}^{L \times d} $

The cross-attention matrix reduce to a self-attention matrix. …

Causal-Attention

Causal-Attention is achieve by causal mask, which will be discussed below.

Causal-Attention is not mutually exclusive with Cross-Attention or Self-Attention. For example, the Transformer decoder contains two attention layers:

• First layer
  • Self-Attention + Causal Attention
  • Auto-regressive: each token attend to the translated sentence, but can only attend to previously generated words
• Second layer
  • Cross-attention
  • Each token in the translated sentence can attend to any tokens in the source sentence

One can imagine designing an architecture using “Cross-attention + Causal Attention”, i.e., the output sequence can only attend to current step in the input sequence.

Implementation

The above 3 types of Attentions can be implemented by a single function. Check Harvard NLP’s implementation for details.

Analysis

Kernel Function

\[K: \mathbb{R}^d \times \mathbb{R}^d \rightarrow \mathbb{R}\]

As discussed in the Attention post, a kernel function can be a dot product (linear kernel):

\[K(x,y) = x^\top y\]

The Transformer uses a modified Softmax kernel:

\[K(x,y) = \exp \left( \frac{x^\top y}{\sqrt{d}} \right)\]

The story I heard is the researcher first tried linear kernel on NMT problem, but it did not work well. The reason they suspect is that attention in NLP should be sparse: the target token is strongly correlated to some tokens and has zero correlation to others. This requires a more “sharp” kernel.

A natural way to amplify a value is to take exponential and the softmax function is commonly used to approximate the $\operatorname{argmax}$ function. However, a naive softmax kernel creates stability problem: considering $d=64$, a dot product $x^\top y$ could produce a large scalar and taking an exponential leads to a numerical overflow.

The modified Softmax kernel normalize the dot product by $\sqrt{d}$. The constant $\sqrt{d}$ is not just a heuristic design choice: at the beginning of training, $W$ is initialized as $W \overset{inp}{\sim} N(0,1)$. Assume input is normally distributed, then $Q, K \overset{inp}{\sim} N(0,1)$, hence each $x,y \overset{inp}{\sim} N(0,1)$.

The expectation $\mathbb{E}[x^\top y] = \mathbb{E}[ \sum_{i=1}^d X_i ] $ where $X_i \overset{inp}{\sim} N(0,1)$. By concentration inequality or central limit theorem, $P( x^\top y \geq \sqrt{d} )$ is very small.

Other than the softmax kernel, one can use the ReLU kernel:

\[K(x,y) = \operatorname{ReLU}(x)^\top \operatorname{ReLU}(y)\]

The ReLU kernel is fast, but less accurate than the softmax kernel in empirical experiments.

Complexity

A major problem of the Transformer is its computation does not scale linearly on sequence length $L$.

The computation cost of the attention matrix $Q K^\top$ is $O(L^2d’)$, where $ Q \in \mathbb{R}^{L \times d’} $ and $ K \in \mathbb{R}^{M \times d’} $. For extremely long sequence (e.g., music data with length in thousands, or DNA sequencing data with length in millions), the quadratic complexity is not acceptable. See Table 1 of the Music Transformer paper for details.

Recent works explores the possibility of low rank approximation of the softmax kernel function:

\[A = \exp(QK^\top / \sqrt{d'}) \approx \mathbb{E}[ Q' \cdot (K')^\top ]\]

The advantage is instead of first computing $A = QK^\top$ then $X’=AV$, we can first compute $B=(K’)^\top V$, then $X’=Q’B$. This result in a linear complexity $O(Ldd’)$.

For details, readers can check the Performer paper.

Masking

Reader may need to distinguish the attention mask from the input mask in Masked Language Models (MLM).

• Attention mask: set specific values of the attention matrix to zero
• Input mask in MLM: set certain tokens in the input sequence to a pre-assigned [MASK] token
  • The encoder’s attention matrix is not affected.

No Mask

As the name suggested, the attention matrix is passed as it is, implying each word can attend to any words in the entire sequence.

Causal Mask

The attention matrix is masked by a lower triangular matrix, implying each word can only attend to words before it.

Positional Encoding

The Attention operation does not contains ordering information of the sequence (i.e., a weighted sum of value matrix $V$, where weights are compute from $Q,K$ using a kernel function). Positional encoding (PE) was used to inject information of relative or absolute position into the input sequence.

A valid PE should: encode a unique vector for each position in the sequence.

Two variants are proposed:

• Absolute Positional Encoding (APE): inject the positional information into the input sequence
• Relative Positional Encoding (RPE): inject the positional information into the attention matrix

In music generator task, RPE significantly outperforms APE.

Absolute Positional Encoding (APE)

APE was proposed in the Attention Is All You Need paper. It directly inject the positional information into the input sequence.

Suppose the input embedding is $d$ dimensional. APE create a $d$ dimensional vector and add this vector to the input embedding.

The authors uses sine and cosine functions of different frequencies as APE:

\[\operatorname{PE}(pos, 2i) = \sin(\frac{pos}{10000^{ 2i/d} } )\] \[\operatorname{PE}(pos, 2i+1) = \cos(\frac{pos}{10000^{ 2i/d} } )\]

where $pos$ is the position, and $2i$ / $2i+1$ is the dimension. The wavelengths of sine and cosine function form a geometric progression from $2\pi$ (dimension 0 and 1) to $10000 \cdot 2\pi$ (dimension 510 and 511).

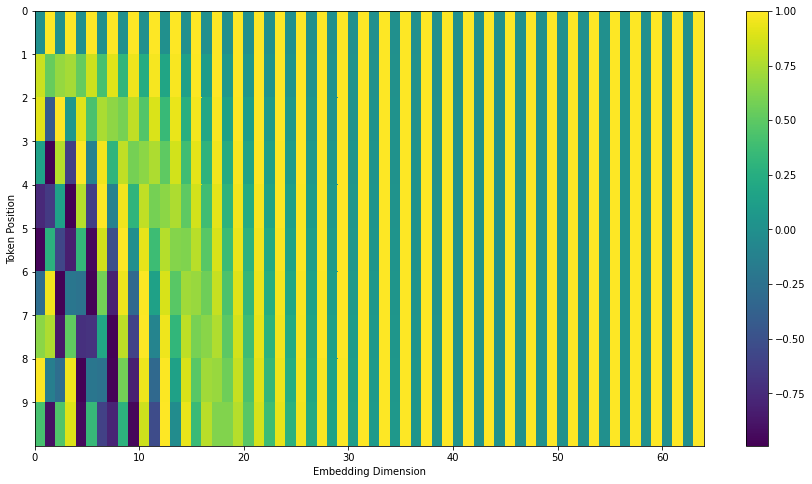
Visualization of positional encoding from Jay Alammar’s blog. y-axis: position 0-9; x-axis: APE vector’s dimension 0-64.

Relative Positional Encoding (RPE)

• Self-Attention with Relative Position Representations, 2018
• Music Transformer: Generating Music with Long-Term Structure, 2018
• Relative Positional Encoding for Transformers with Linear Complexity, PMLR 2021

RPE was proposed and refined in the above two 2018 papers and adapt to the kernel approximation method in the 2021 paper.

Given the attention matrix $A$ where

\[A_{ij} = \exp(\frac{q_i k_j^\top}{ \sqrt{d} })\]

The idea is directly encoder the relative positional information to the attention matrix:

\[\widetilde{A}_{ij} = A_{ij} \cdot f_\theta(i-j) = \exp(\frac{q_i k_j^\top + \sqrt{d}\log f_\theta(i-j)}{ \sqrt{d} }) = \exp(\frac{q_i k_j^\top + R_{ij}}{ \sqrt{d} })\]

where $f_\theta: \mathbb{R} \rightarrow \mathbb{R}$ is a learnable function with parameter $\theta$ and $R_{ij}$ is a Toeplitz matrix which encodes the relative positional information. The reason to express $f_\theta$ in a matrix $R$ is to utilize matrix parallel processing.

In the original paper the RPE also take value of $Q$ into consideration:

\[A_{ij} = \exp(\frac{q_i k_j^\top + q_i (R_{ij})^\top}{ \sqrt{d} })\]

Architecture

A detailed discussion of Encoder and Decoder design of Transformer:

Normalization

Transformer uses layer normalization. The reason is that, batch normalization is inefficient for a batch of variable length sequences. More discussions can be found at [TBD].

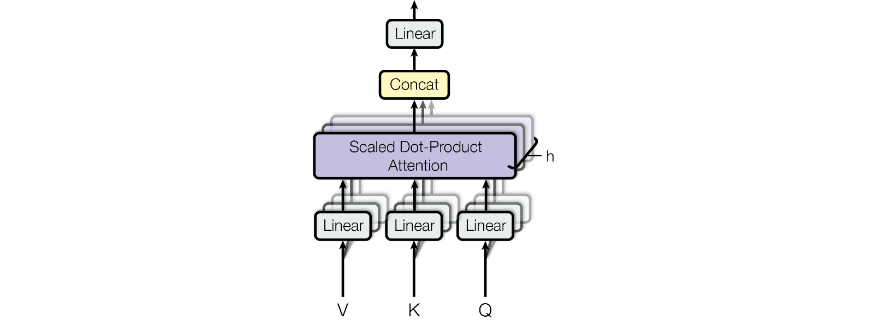
Multi-Head Attention

The idea of Multi-Head Attention is that each attention block can focus on one type of relationship. This is analogous to having multiple channels in CNN. By random initialization, attention blocks are likely being optimized to find different patterns after training.

Each of the $h$ attention heads maintains its own $W_q, W_k, W_v$. The Concat layer pools information from different heads together and Linear layer applies a transformation on the combined information.

Encoder - Decoder

Encoder and decoder contains stacks of $N$ EncoderLayer and DecoderLayer.

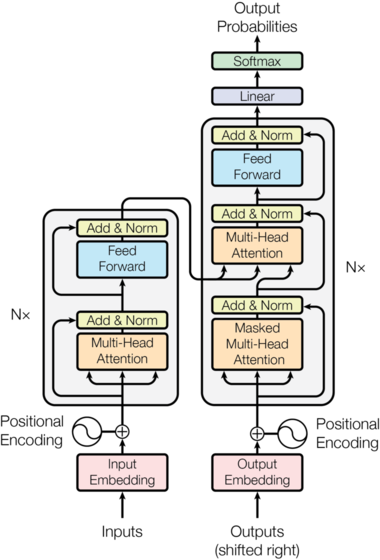
The Transformer - model architecture

EncoderLayer

• Multi-Head Self-Attention
• Skip connection + Layer Normalization
• Feed-Forward Networks
• Skip connection + Layer Normalization

DecoderLayer

• Multi-Head Causal-Attention
• Skip connection + Layer Normalization
• Multi-Head Cross-Attention
• Skip connection + Layer Normalization
• Feed-Forward Networks
• Skip connection + Layer Normalization

Feed-Forward Networks

• Linear
• ReLU
• Dropout
• Linear

Attention class contains a Dropout parameter, which applies dropout to the attention matrix.

Different configuration of encoder/decoder blocks result in architectures:

• Transformer: stacked encoder blocks and decoder blocks
• BERT: stacked encoder blocks
• GPT: stacked decoder blocks