K-Means
This post is mainly based on
Clustering
Clustering is a class of unsupervised learning algorithms. The goal is to group a set of points into clusters s.t., points in the same cluster are similar; points in different clusters are dissimilar. A distance measure is require to measure similarity.
The distance measure could be L2-distance, leading to Centroid-Based Clustering; it could also be probability, leading to Distribution-Based Clustering; modern algorithms use reachability/connectivity as the distance measure, leading to Density-Based Clustering. We can also aggregate results from multiple clustering algorithms/runs to create cluster ensembles, leading to Consensus Clustering. Consensus clustering for unsupervised learning is analogous to ensemble learning in supervised learning.
K-means Clustering
Given a set of points $x_1, x_2, …, x_n \in \mathcal{X}$ and number of groups $k$, find a set of cluster $C = \{ C_1, …., C_k \}$ with centroids $c_1, …, c_k$, s.t., the within-cluster sum of squares (WCSS) is minimized:
\[C = \operatorname{argmin}_{C_1, ..., C_k} \sum_{j = 1}^k \operatorname{WCSS}(C_j)\] \[\operatorname{WCSS}(C_j) = \sum_{x \in C_j} \| x - c_j \|^2\]or
\[c_1, ..., c_k = \operatorname{argmin}_{c_1, ..., c_k}\left[ \sum_{i=1}^n \operatorname{min}_{j=1, ..., k} \| x_i - c_j \|^2 \right]\]The assigned cluster $j$ for point $x_i$ is $\operatorname{argmin}_j \| x_i - c_j \|^2 $. Unfortunately problem is NP-hard and there is no efficient algorithm to find a global minimum.
Lloyd’s Algorithm
Lloyd’s Algorithm is an algorithm to approximate K-means. It adopts an iterative procedure to improve fitting:
- Initialization: Initialize cluster centroids $c_1, …, c_k$ (randomly or K-Means++)
- Repeat until convergence
- Assignment: for each $x$, assign to its closest cluster, $x \in C_j$, where $j = \operatorname{argmin}_j \| x_i - c_j \|^2$
- Update: for each cluster, compute its centroid $c_j = \frac{1}{|C_j|} \sum_{x \in C_j} x $
Problems of Lloyd’s Algorithm
- The approximation can be arbitrarily bad compared to the optimal clustering, and the quality of clustering depends on the initialization
- Speed of convergence: in the worst-case, Lloyd’s algorithm needs $2^{\Omega(n)}$ iterations to converge; although, in practice, the number of iterations until convergence is often small
Other approximation algorithm: MacQueen’s algorithm, Hartigan-Wong method. If you are interested in more details, check out this article.
K-means++
K-means++ was proposed in 2007 to tackle the first problem of Lloyd’s Algorithm: avoid poor initialization. The intuition is to spreading out clusters:
- Choose the first cluster centroid from all points $x_1, …, x_n$ randomly
- For the remaining $1-k$ clusters
- Choose the cluster centroid with probability proportional to its squared distance from the point’s closest existing cluster: $p(x_i) = \frac{D(x_i)^2}{\sum_i D(x_i)^2}$
The authors found that k-means++ consistently outperformed random initialization both in speed and WCSS (they called potential function $\phi$) in 4 datasets (real and synthetic). They also provided an upper bound for the WCSS $\mathbb{E}[\phi] \leq 8(\ln k + 2) \phi^*$ (although this bound is not really tight). Check out the original paper for more details.
Number of Clusters $k$
Determining number of clusters $k$ in very important in practice, but it is rarely discussed.
ELBOW Method
Most introductory articles suggest using ELBOW Method. ELBOW Method plot WCSS against number of cluster $k$. As $k$ increases, $\text{WCSS}$ decrease, since you can always split one of the optimal $k-1$ clusters and produce a lower WCSS for the cluster you destroyed. The ELBOW Method suggest that $k$ should be chosen s.t. there is a sharp change in slope:
\[\text{WCSS}_k - \text{WCSS}_{k-1} \ll \text{WCSS}_{k+1} - \text{WCSS}_{k}\]The intuition is that $k$ should be chosen s.t., increasing number of cluster does not result in tighter groups. However, you will probably find the WCSS curve is rather smooth in practice. Identifying the ELBOW point is non-trivial.
Gap Statistics
Gap statistics was proposed for determining the optimal number of cluster. Gap statistics compares the shape of WCSS obtained from running clustering algorithm on the target dataset to the shape of WCSS obtained from running clustering algorithm on a null reference distribution. A null reference distribution is a uniform distribution that has no ground truth cluster structure. As discussed in the ELBOW Method section, as $k$ increase, $\text{WCSS}$ will decrease in a smooth curve even when there is no ground truth cluster structure.
The idea of the Gap Statistics is compare the gap between the WCSS of target dataset to the WCSS of the null reference distribution. When the this gap begin to shrink larger than some margin of error, it is highly likely that the decrease in WCSS of target dataset originate from splitting some uniform distribution within a well defined, ground truth cluster. Therefore, the optimal $k$ should be the $k$ before this shrink in gap begins to occur. Below is a figure from the original paper:
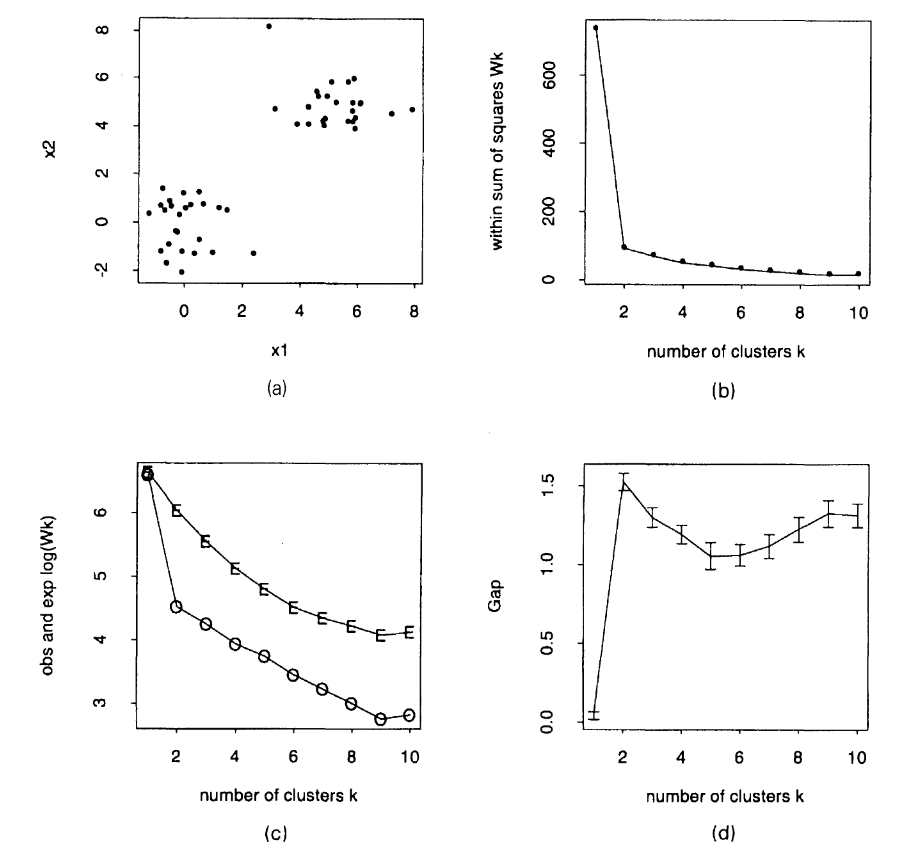 Figure (a): target dataset. Figure (b): WCSS of the target dataset. Figure (c): $\log(\text{WCSS}); $”O” stands for the target dataset and “E” stands for the expected or simulated dataset. Figure (d): Gap statistics curve with the margin of error $s_{k+1}$ plotted as error bars.
Figure (a): target dataset. Figure (b): WCSS of the target dataset. Figure (c): $\log(\text{WCSS}); $”O” stands for the target dataset and “E” stands for the expected or simulated dataset. Figure (d): Gap statistics curve with the margin of error $s_{k+1}$ plotted as error bars.
Observe that speed of WCSS drop dramatically slow down after for $k \geq 2$. This result in the gap between target and reference WCSS to shrink.
Computation
We will simulate $B$ reference datasets by Monte Carlo simulation. The easiest way to simulate the datasets is to sample uniformly random over the range of the observed data. Let:
- $W_k$ = WCSS of the $k$ clusters derived from the target dataset
- $W_{kb}^*$ = the expectation of WCSS of the $k$ clusters derived from the $B$ simulated reference datasets
- $\text{sd}_k$ = the standard derivation of the simulated WCSS
- $s_k = \sqrt{1 + \frac{1}{B}} \text{sd}_k$
Gap statistics is computed as:
\[Gap(k) = \frac{1}{B} \sum_b \log(W_{kb}^* - \log(W_k))\]Choose the number of cluster as:
\[\hat{k} = \text{smallest }k\text{, such that, } Gap(k) \geq Gap(k+1) - s_{k+1}\]There are many design choices made in this paper, for example: why choosing 1-standard derivation as error margin? why choosing the $\log(\text{WCSS})$? Variants of Gap statistics were proposed and discussed. If you are interested in more details, check out this paper.