MCMC could be inefficient due to high rejection rate. Do we have an MCMC algorithm which did not reject any sample? Yes, it is Gibbs Sampling. To achieve this, Gibbs sampling update each coordinate conditioned on the rest of coordinates. Intuitively, you can think of it as the coordinate descent modified to samples points rather than finding the minimum. Its update rule requires conditional distribution for all dimensions (you can also update multiple dimensions together).

MCMC

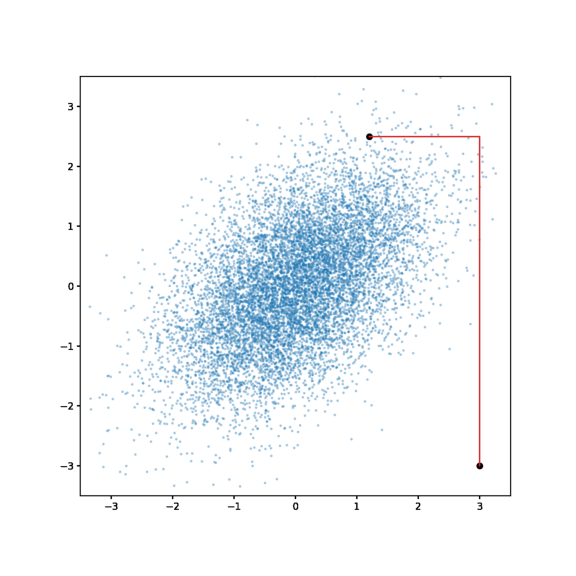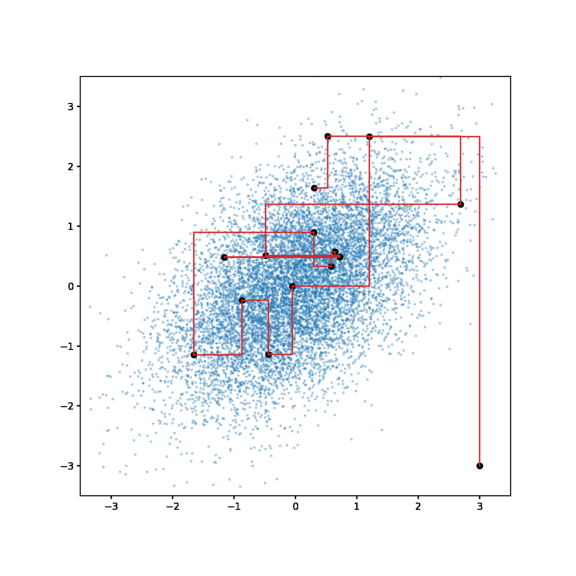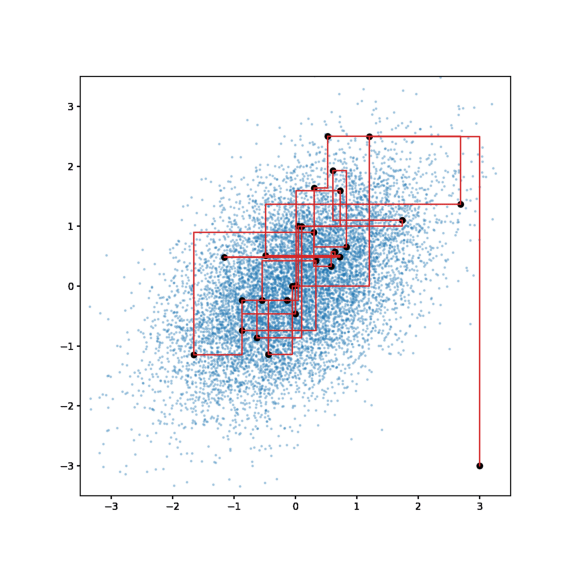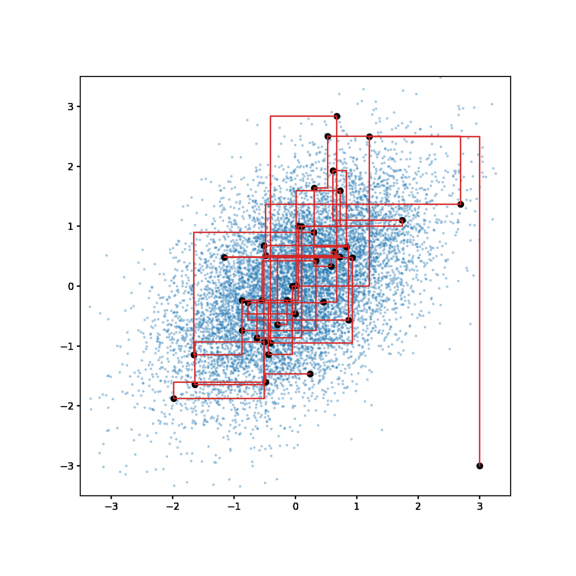
Algorithm

Notation: $x^i_j$ represent $j$-th dimension of $i$-th sample in chain

  • Initialize the chain to $x^1$
  • Sample for each dimension of the joint distribution
    • $x^{t+1}_1 \sim p(x_1 | x^t_2, x^t_3, …, x^t_p)$
    • $x^{t+1}_2 \sim p(x_2 | x^{t+1}_1, x^t_3, …, x^t_p)$
    • $x^{t+1}_3 \sim p(x_3 | x^{t+1}_1, x^{t+1}_2, …, x^t_p)$
    • …
    • $x^{t+1}_p \sim p(x_p | x^{t+1}_1, x^{t+1}_2, …)$

A special case of Metropolis–Hastings

Gibbs sampling is a special case of Metropolis–Hastings in which the newly proposed state is accepted with probability one. Let $x_d = d$-th dimension of $x$ and $x_{-d} = x$ without the $d$-th dimension. Then Gibbs sampler generate proposal by $p(x_d | x_{-d})$.

Recall MH’s acceptance probability: $A(x_t \rightarrow x’) = \operatorname{min}(1, \frac{f(b)}{f(a)} \frac{g(a | b)}{g(b | a)})$.
In Gibbs sampler

  • $f(x) = f(x_d, x_{-d}) = f(x_d | x_{-d})f(x_{-d})$
  • $g(x | x_t) = f(x_d | x_{-d}, x_t) = f(x_d | x_{-d})$
\[\frac{f(b)}{f(a)} \frac{g(a | b)}{g(b | a)} = \frac{f(b_d | a_{-d})f(a_{-d}) f(a_d | a_{-d})}{f(a_d | a_{-d})f(a_{-d}) f(b_d | a_{-d})} = 1\]

Therefore, Gibbs Sampler’s acceptance probability: $A(x_t \rightarrow x’) = \operatorname{min}(1,1) = 1$

Summary

  • Gibbs Sampling does not requires a proposal distribution
  • Gibbs Sampling is efficient when you can efficiently sample from conditional distributions
    • Gibbs Sampling is efficient when conditionals are conjugates
    • If conditionals are not tractable, you still need to run a need to a rejection sampling or a Metropolis-Hastings steps to sample each dimension
  • There are many classical Bayesian inference problem which can be efficiently solved by Gibbs Sampling
    • Hierarchical normal model
    • Bayesian linear regression
    • Multivariate normal model
    • Mixture model

This post has more discussions on Gibbs Sampler and its variants.