Balls in the Hat
I encountered this interesting problem at a guest lecture by Dr. Ranjan Bhaduri. A detailed discussion can be found here.
Consider a hat with $b$ black balls and $w$ white balls. At each round, you draw a ball from the hat without replacement. You gain \$1 for each white ball drawn from the hat and suffer \$1 loss for each black ball draw from the hat. You can stop the game at any time or until all balls are drawn. Should you play this game if there are $6$ black balls and $4$ white balls in the hat?
At first glance, most people would refuse to play. However, you should play this game since the expected return is $+\frac{1}{15}$. The reason is that you can choose to stop at any time. Consider the following 3 cases:
- 1 black, 0 white
- You should stop and your expected return is 0
- 0 black, 1 white
- You should play and your expected return is 1
- 1 black, 1 white
- $P(\text{draw white}) = 0.5$; You gain \$1 at this round and you go to case “1 black, 0 white”, where you stop.
- $P(\text{draw black}) = 0.5$; You lose \$1 at this round and you go to case “0 black, 1 white”, where you play and gain \$1.
- Your expected return is $+0.5$
This problem can be solve by dynamic programming:
\[\mathbb{E}[b,w] = \operatorname{max}\left( \left[\frac{w}{b+w}(1+\mathbb{E}[b,w-1]) + \frac{b}{b+w}(-1+\mathbb{E}[b-1,w])\right], 0 \right)\]Below is the return matrix where row index is number of black balls and column index is number of white balls. Return on Row 6 column 4 is $0.067 = \frac{1}{15}$. Implementation can be found here.
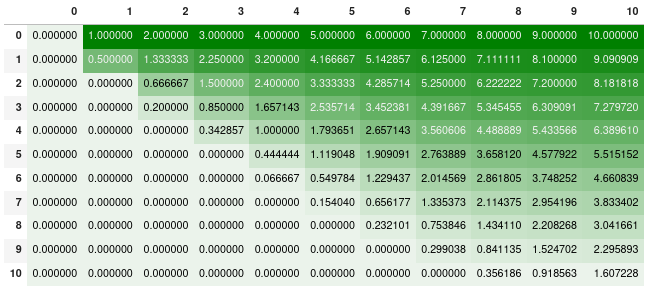
Note that the expected return for “1 black, 1 white” case is positive rather than $0$. This illustrated that the player’s right to stop has value. The author draw analogy between this game and investing: By acting optimally the player can participate in all of the upside of drawing more than the expected number of white balls while not fully participating in the downside of drawing more than the expected number of black balls. However, most portfolio managers conduct statistical analysis to compare the two (mean, standard deviation, skew, kurtosis, Sharpe, Omega, etc.) while ignoring the difference in liquidity (the ability to pull money at desired time).