This post is mainly based on

Overview

  • Question
    • How to measure the capacity of a model?
    • How many parameters are really needed?
  • “Suggestive” Conclusion
    • Many problems have smaller intrinsic dimensions than one might suspect
    • The intrinsic dimension for a given dataset varies little across a family of models with vastly different sizes
    • Implication: once a parameter space is large enough to solve a problem, extra parameters serve directly to increase the dimensionality of the solution manifold
  • Intrinsic dimension allows quantitative comparison across different types of learning (e.g., supervised, reinforcement)
    • Solving the inverted pendulum problem is 100 times easier than classifying digits from MNIST
    • Playing Atari Pong from pixels is about as hard as classifying CIFAR-10
  • Intrinsic dimension can be used to obtain an upper bound on the minimum description length of a solution
    • By product: compressing, low dimensional representation

NN Optimization

  • Steps
    • Step 1: Fix dataset, network architecture, loss function
    • Step 2: Initialize network
    • Step 3: Adjusting its weights to minimize loss
  • “Training NN” = traversing some path along an objective landscape (loss landscape)
  • As soon as Step 1 is completed, the loss landscape is fixed
  • Step 2 and 3 only affect how the loss landscape is explored
  • Dimension of the optimization
    • Given a network parameterized by $D$ parameters
    • The optimization problem is $D$ dimensional

Background

Toy Example 1

  • $\theta_1 + \theta_2 + \theta_3 = 1$
  • Parameter space: $\theta \in \mathbb{R}^3$
  • Intrinsic dimension: 1 or $\mathbb{R}$
  • Why?
    • The manifold of the solution space is a hyperplane passing through $(0,0,1)$, $(0,1,0)$ and $(1,0,0)$
    • This manifold is 2 dimensional
    • Denoting as $s$ the dimensionality of the solution set
    • $D = d_{int} + s$. Hence the codimension $d_{int} = 3-2 = 1$
  • On the manifold, there are 2 orthogonal directions one can move and remain at zero cost

Toy Example 2

  • $D = 1000$
  • Loss: Squared error cost function that requires,
    • The first 100 elements to sum to 1
    • The second 100 elements to sum to 2
    • …
  • The manifold of solutions is a 990 dimensional hyperplane
  • $d_{int} = 10$

$d_{int}$ approximation

  • For hard optimization problem: need algorithm method to approximate $d_{int}$
  • Notations
    • Parameter: $\theta^{(D)} \in \mathbb{R}^D$
    • Initial parameter: $\theta^{(D)}_0$
    • Final parameter: $\theta^{(D)}_*$
    • Projection matrix: $P$, randomly generated and frozen
    • Some paper called $\theta^{(d)}$ a $\theta^{(D)}$
  • Training: $\theta^{(D)} = \theta^{(D)}_0 + P(\theta^{(d)})$
  • Choice of $P$
    • $P = \theta^d W$
    • $P = \theta^d W_{sparse}$
    • $P = \theta^d M$, Fastfood transform
      • $M = HG \Pi HB$, fixed
      • $H$: a Hadamard matrix
      • $G$: a random diagonal matrix with independent standard normal entries
      • $B$: a random diagonal matrix with equal probability $\pm 1$ entries
      • $\Pi$: a random permutation matrix
      • Matrix multiplication with a Hadamard matrix can be computed in $O(D \log d)$ via the Fast Walsh-Hadamard Transform
  • Training proceeds by computing gradients with respect to $\theta^{(d)}$
    • To compute gradient w.r.t $\theta^{(d)}$
    • Take an extra step in chain rule to compute $\partial \theta^{(D)} / \partial \theta^{(d)}$
  • Choice of $P$
    • Columns of P are normalized to unit length
    • Columns of P may also be orthogonalized if desired (paper use approximate orthogonality)
  • Adjustment to optimizers
    • SGD is “rotation-invariant”
    • For RMSProp & Adam, the path taken through $\theta^{(D)}$ space will depend on the rotation chosen
  • Can we find solution in subspace $\theta^{(d)}$?
    • If $d < D-s$, solutions will almost surely not be found (with probability 1)
    • If $d \geq D-s$,
      • If solution set is a hyperplane, the solution will almost surely intersect the subspace
      • If solution set has arbitrary topology, intersection is not guaranteed

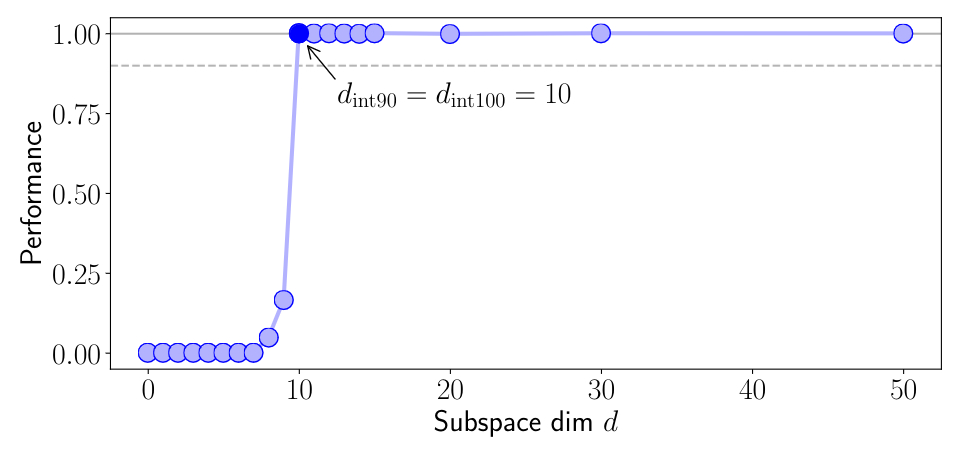
toy-ex-2

Plot of performance vs. subspace dimension for the toy example 2. The problem becomes both 90% solvable and 100% solvable at random subspace dimension 10, so $d{int90}$ and $d_{int100}$ are 10._

$d_{int}$ Details

  • $d_{int100}$: solutions whose performance is statistically indistinguishable from baseline solutions
    • $d_{int100}$ tends to to vary widely
    • $d_{int100} \rightarrow D$ when the task requires matching a very well-tuned baseline model
  • $d_{int90}$: solutions with performance at least 90% of the baseline
    • More practical and useful

Experiments: MNIST

Compression

  • FC and CNN are very compressible
  • Store
    • The random seed to generate the frozen $\theta^{(D)}$
    • The random seed to generate $P$
    • The 750 floating point numbers in $\theta^{(d)}_*$
  • FC
    • 750 degrees of freedom (0.4% params) for 90% of the baseline performance
    • Assuming fp32, compression factor = 260x (from 793kB to only 3.2kB)
  • CNN (LeNet)
    • 290 degrees of freedom (0.65% params) for 90% of the baseline performance
    • Assuming fp32, compression factor = 150x

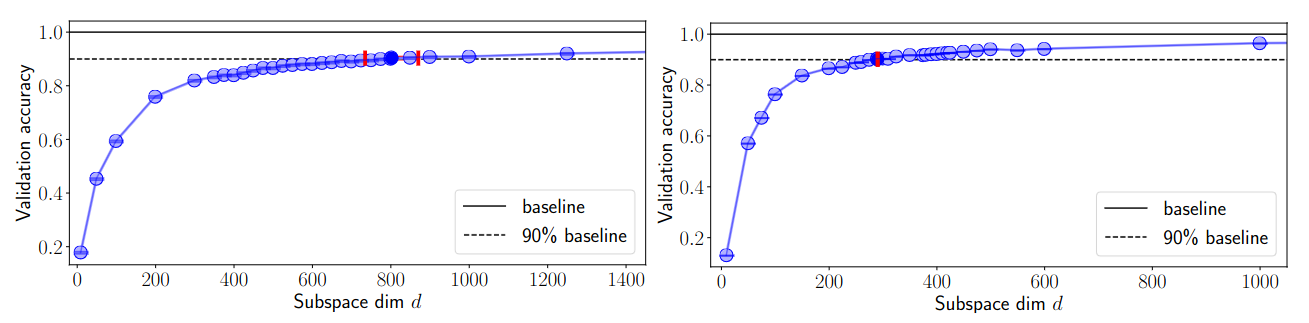
mnist-dim

Performance (validation accuracy) vs. subspace dimension d for two networks trained on MNIST. Left: FC; Right: CNN.

Robustness of Intrinsic Dimension

  • How intrinsic dimension varies across FC networks with a varying number of layers and varying layer width
  • Grid sweep on FC
    • Layers $L \in {1, 2, 3, 4, 5}$
    • Width $W \in {50, 100, 200, 400}$
  • Results
    • $D$ changes by a factor of 24.1
    • $d_{int90}$ changes by a factor of 1.33

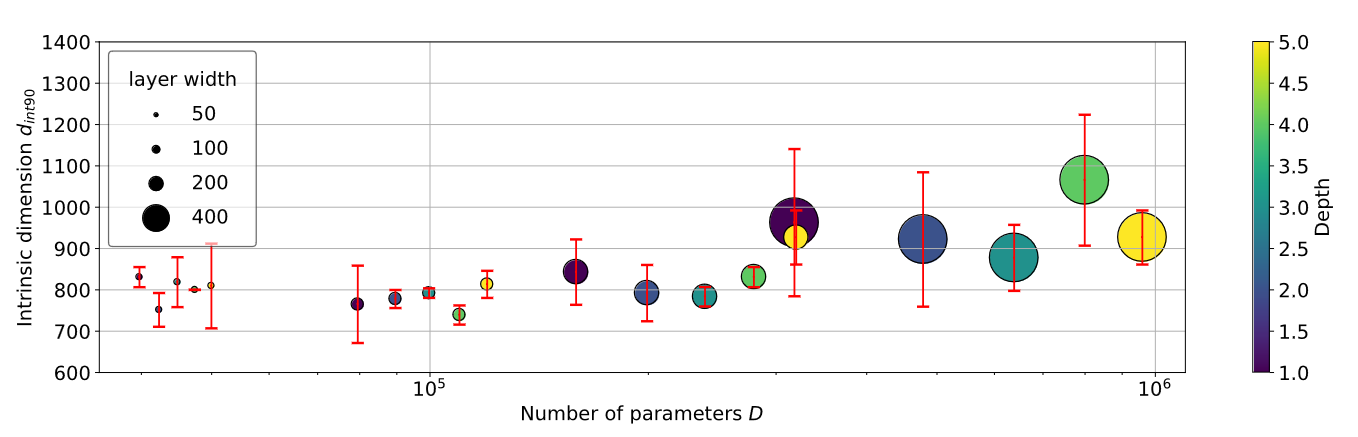
robust

Intrinsic dimension vs number of parameters for 20 FC models. Though the number of native parameters $D$ varies by a factor of 24.1, \(d_{int90}\) varies by only 1.33. This indicate that \(d_{int90}\) is a fairly robust measure across a model family.

Random Subspaces Parameter Efficiency

  • If the intrinsic dimension for MNIST is low, can we directly train a small network, instead of train in subspace of large network?
  • 1000 small networks
    • Layers $L \in {1, 2, 3, 4, 5}$
    • Width $W \in {2, 3, 5, 8, 10, 15, 20, 25}$
  • Results
    • FC: Given the same level of validation accuracy, there persistent horizontal gap given similar # of trainable parameters
    • CNN: generally more parameter efficient than FC

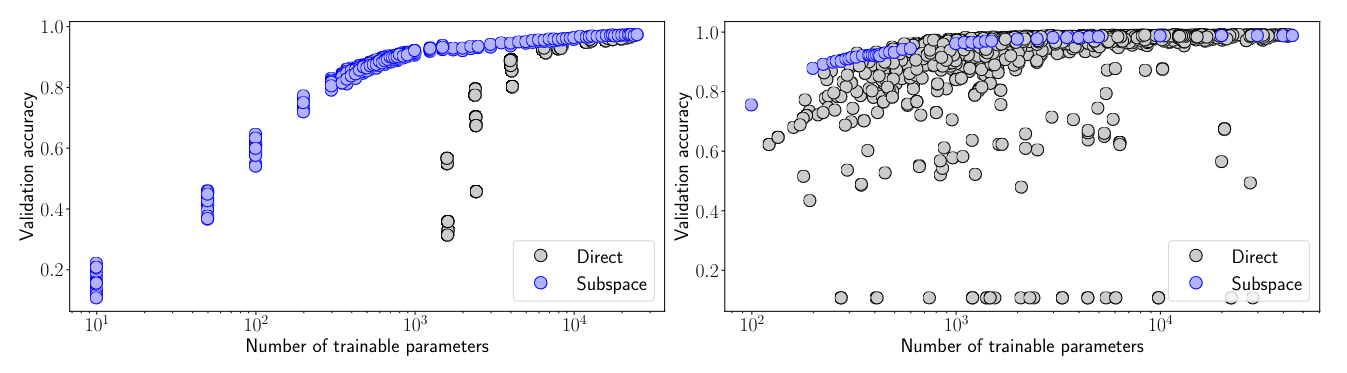
param-eff

Performance vs. number of trainable parameters for (left) FC networks and (right) CNN trained on MNIST. Gray circles: randomly generated direct networks. Blue circle: random subspace training results. CNN: parameter efficiency varies, as the gray points can be significantly to the right of or close to the blue manifold.

Measuring $d_{int90}$ on Shuffled Data

  • Compared to FC, CNN impose inductive bias. So are CNN always better than FC on MNIST?
  • Shuffled Data: pixels are subject to a random permutation, chosen once for the entire dataset
  • Results
    • FC: $d_{int90}$ remains at 750
    • CNN: $d_{int90}$ jump from 290 to 1400
  • Catch
    • CNN better suited to classifying digits given images with local structure
    • When this structure is removed, violating convolutional assumptions, more degrees of freedom are now required to model the underlying distribution

Experiments: Various Learning Problems

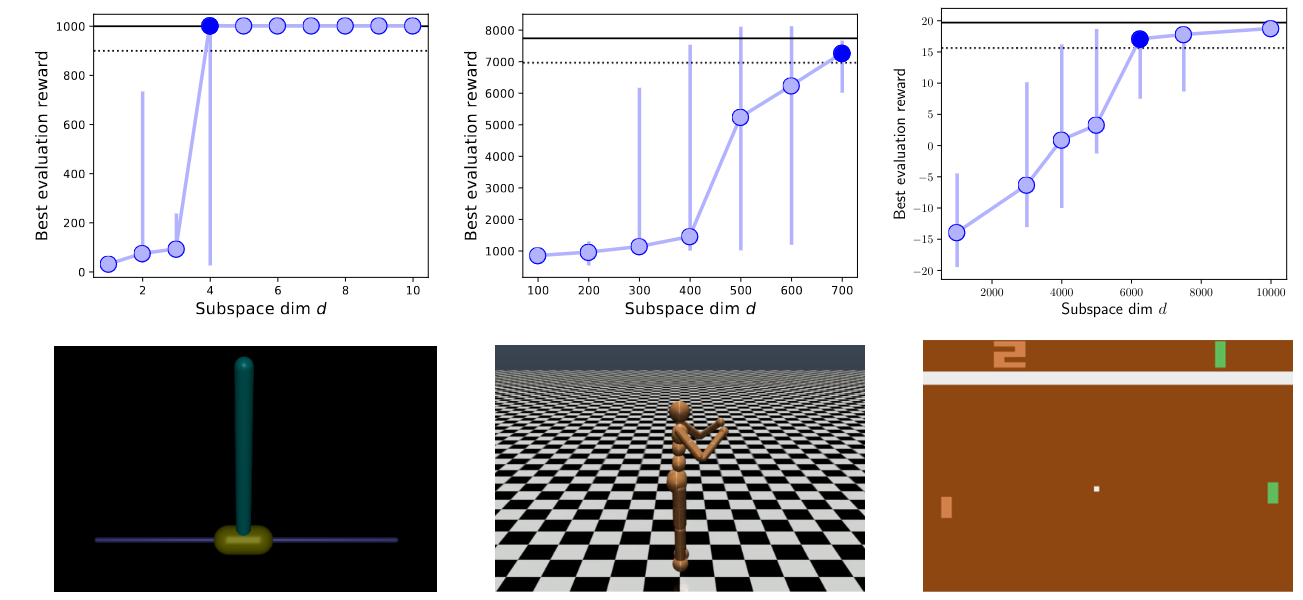
param-eff-rl

Intrinsic dimensions on InvertedPendulum−v1, Humanoid−v1, and Pong−v0. This places the walking humanoid task on a similar level of difficulty as modeling MNIST with a FC network. Pong on the same order of modeling CIFAR-10.

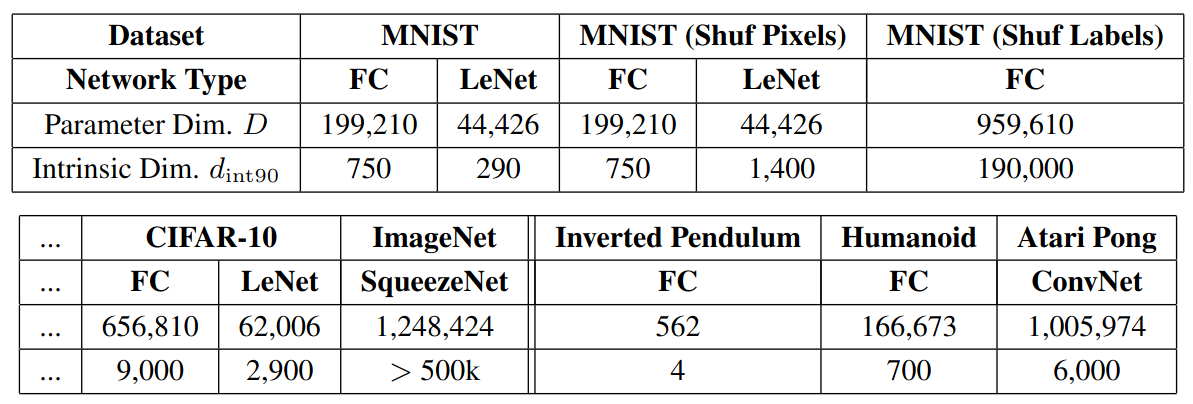
param-eff-comp

\(d_{int90}\) measured on various supervised and reinforcement learning problems.