Online Softmax
This post is mainly based on
Online Softmax
- Modern GPU are mostly I/O bounded, not compute bounded
- Parallel Online Softmax achieves 1.3x speed up by reducing memory I/O
- Fusing Softmax + TopK achieves 5x speed up by further reducing memory I/O
Naive Softmax
Softmax is the default method of converting a score vector into a probability vector
\[y_i = \frac{ e^{x_i} }{ \sum e^{x_j} }\]where $x,y \in \mathbb{R}^V$
Let $d_V = \sum e^{x_j} $, a naive softmax algorithm runs 2 loops
- Compute the $d_V$ in the first loop: $d_j \leftarrow d_{j-1} + e^{x_j}$
- Compute $y_i$ in the second loop: $y_i \leftarrow e^{x_i} / d_V$
This induce 2 $O(V)$ read and 1 $O(V)$ write.
Safe Softmax
On real hardware, the large sum $d_V$ can overflow. Therefore, a safe softmax can be computed as follow
Let $m_V = \max x_i$
\[y_i = \frac{ e^{x_i} }{ \sum e^{x_j} } \cdot \frac{e^{-m_V}}{e^{-m_V}}= \frac{ e^{x_i - m_V} }{ \sum e^{x_j - m_V} }\]This ensures that all elements of the running sum: $e^{x_j - m_V} < 1$. Therefore, the full precision FP32 $d_j$ is guaranteed to not overflow for sum of $V < 1.7 \cdot 10^{37}$ elements.
All major DL frameworks are using this safe version for the Softmax computation. However, the safe softmax requires additional memory access:
- Compute $m_V$ in the first loop: $m_k \leftarrow \max(m_{k−1}, x_k)$
- Compute $d_V$ in the second loop: $d_j \leftarrow d_{j-1} + e^{x_j - m_V}$
- Compute $y_i$ in the third loop: $y_i \leftarrow e^{x_i - m_V} / d_V$
This induce 3 $O(V)$ read and 1 $O(V)$ write.
Online Softmax
The Online softmax seek to reduce the 3 $O(V)$ read to 2 $O(V)$ read.
- The problem is computing $d_V$ requires $m_V$: $d_j \leftarrow d_{j-1} + e^{x_j - m_V}$
The online version compute $d_V$ and $m_V$ in 1 loop:
\[m_j \leftarrow \max(m_{j-1}, x_j)\] \[d_j \leftarrow d_{j-1} \times e^{m_{j-1} - m_j} + e^{x_j - m_j}\]Essentially, the online normalizer trade memory access with additional compute: adjusting the $d_{j-1}$ term with scaling factor on the fly.
Parallel Online Softmax
Define a generalized version of the online normalizer calculation:
\[\begin{bmatrix} m_V \\ d_V \end{bmatrix} = \begin{bmatrix} x_1 \\ 1 \end{bmatrix} \oplus \begin{bmatrix} x_2 \\ 1 \end{bmatrix} \oplus ... \oplus \begin{bmatrix} x_V \\ 1 \end{bmatrix}\]where the binary operator $\oplus: \mathbb{R}^2 \times \mathbb{R}^2 \rightarrow \mathbb{R}^2$ is defined as:
\[\begin{bmatrix} m_i \\ d_i \end{bmatrix} \oplus \begin{bmatrix} m_j \\ d_j \end{bmatrix} = \begin{bmatrix} m_{ij} \\ d_i \times e^{m_i - m_{ij}} + d_j \times e^{m_j - m_{ij}} \end{bmatrix}\]where $m_{ij} = \max(m_i, m_j)$
Analysis
- Applying $\oplus$ sequentially from left to right is equivalent to running Online Softmax
- $\oplus$ is associative
- $\oplus$ is commutative
$\oplus$ is associative, therefore GPU can executes pairwise operations in parallel batches:
- First apply pairwise $\oplus$ on element: (1,2), (3,4), …, in parallel batches
- First apply pairwise $\oplus$ on element: (12, 34), (56, 78) …, in parallel batches
- Map-reduce paradigm: time complexity $O(\log V)$
$\oplus$ is commutative, therefore GPU can execute operations regardless of the order in which input elements are processed:
- Different processors may complete tasks at varying times
- GPU do not need to enforce strict synchronization
Fused operation
- The goal of this section is demonstrate the how memory I/O can impact GPU performance
- Algorithm:
- Initialize
- $u \in \mathbb{R}^{K+1}$: topK value holder
- $p \in \mathbb{Z}^{K+1}$: topK index holder
- In the Online Softmax loop
- Compute $m_j$ and $d_j$
- $u_{K+1} \leftarrow x_j$
- $p_{K+1} \leftarrow j$
- Sort $u$ and update $p$ according to $u$
- Return
- Compute $v$ using vector $u$ and scalar $m_V, d_V$
- Output $v$ and $p$ (ignore last dummy element)
- Initialize
Analysis
- Safe Softmax + TopK separately: 4 read and 1 write on all elements
- The fused algorithm: 1 read on all elements and $K$ write
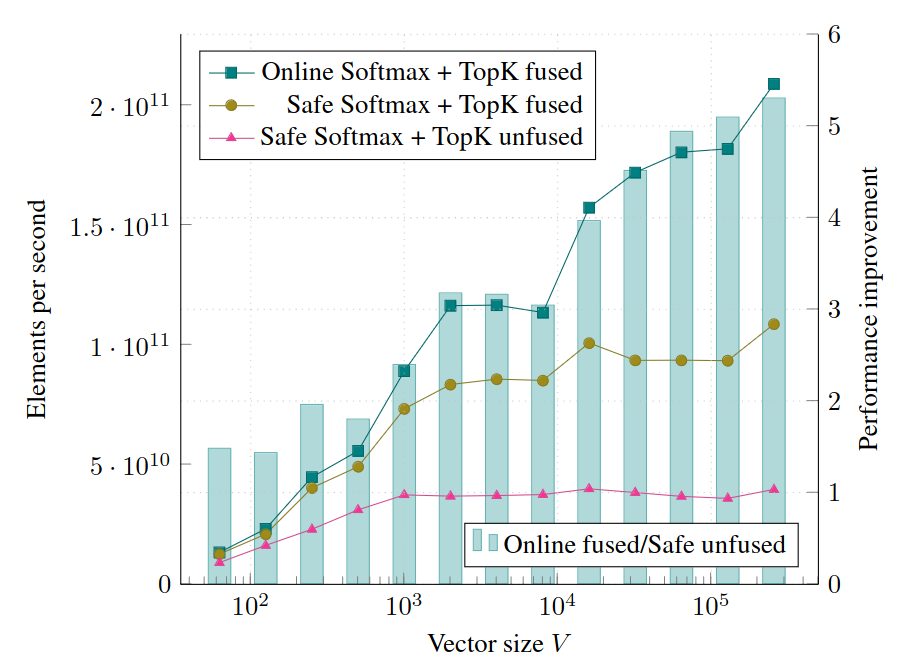
Benchmarking softmax and top-k, Tesla V100, fp32, batch size 4000 vectors. Larger batch results in higher performance.
Memory Efficient Self-attention
- Exact algorithm, not an approximation
- Time complexity: $O(n^2)$; Memory complexity: $O(\sqrt{n})$
- For sequence length 16384, the memory overhead of self-attention is reduced by
- 59x for inference
- 32x for differentiation
Algorithm
Consider the query of a single token against all keys:
\[s_i = q \cdot k_i\] \[s_i' = e^{s_i}\] \[\text{softmax}(q, k_i) = \frac{s_i'}{\sum_j s_j'}\] \[\text{Attention}(q,k,v) = \sum_i \text{softmax}(q, k_i) \cdot v_i = \frac{\sum_i v_i s_i'}{\sum_j s_j'}\]where $q, k_i, v_i \in \mathbb{R}^d$
Hence $s_i, s_i’ \in \mathbb{R}$, $\text{softmax}(q, k_i) \in \mathbb{R}$ and $\text{Attention}(q,k,v) \in \mathbb{R}^d$
Note that, compared to softmax, the Attention algorithm compute the weight sum of all values $[ v_1, …, v_n ]$, using softmax of score $[s_1, …, s_n]$ as weight.
Although the author did not mention the Online Softmax’s paper, their update algorithm over problematic $\text{softmax}$ is essentially the same:
- Initialization
- $m^* = - \inf$
- $v^*$ as zero vector
- $s^* = 0$
- Loop
- $m_i = \max(m^*, s_i)$
- $v^* \leftarrow v^* e^{m^* - m_i} + v_i e^{s_i - m_i}$
- $s^* \leftarrow s^* e^{m^* - m_i} + e^{s_i - m_i}$
- Result
- output = $ v^* / s^* $
Note that the $m^*$ step is essential for numerical stability in GPU hardware since $\text{score} \geq 89$ will cause overflow in bfloat16 and float32.
JAX Implementation
- Support for multiple attention heads and memory-efficient differentiation
- Computation was split into chunk for parallelism
Please refer to paper Figure 1 for the detailed JAX implementation, below is a high level summary:
Split Query into chucks with lax.dynamic_slice()
jax.lax.map() on each query chuck:
Split Key and Value into chucks with jax.lax.dynamic_slice()
jax.lax.map() on each key-value chuck:
Compute element-wise attention scores and softmax for each chuck
Compute intermediate m*, v*, s* at chuck level
Combine chuck level v*, s* into a final v*, s*
// this is the embedding output for each query token within the query chuck
Return v* / s*
Return embedding for all query tokens
Note that jax.lax.map() is design is apply a function to each element of an array in parallel. However, if there is memory constraints, jax.lax.map() might behave more like sequential jax.lax.scan().
Experiments
- Compare memory-efficient attention vs FLAX attention
- Inference
- FLAX attention can handle $2^14k$ or 16k length sequence
- Memory-efficient attention can handle $2^20$ or 1 billion length sequence
- Not much slow down
- Training
- 30% training slow down due to checkpointing
- No performance degradation on measured by BLEU scores
- Query chucking
- Small query chunk size result in poor performance
- For large chunk sizes, the loss of performance is less significant

Memory and time requirements of self-attention during inference.
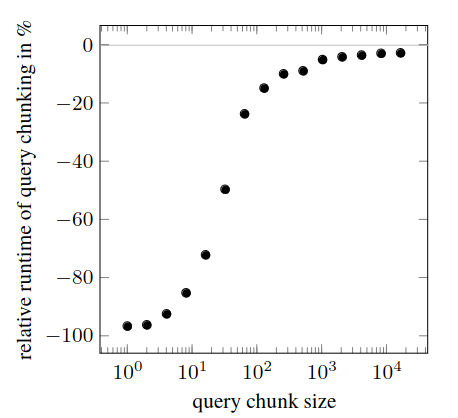
Relative runtime of self-attention on sequence length $2^{15}$ using query chunking compared to standard attention.
Limitations
- Choice of query_chunk_size and key_chunk_size are left to programmer
- Author claims that they do not observe speed similar to FlashAttention due to TPUs are already optimized for compute FLOPs and memory bandwidth